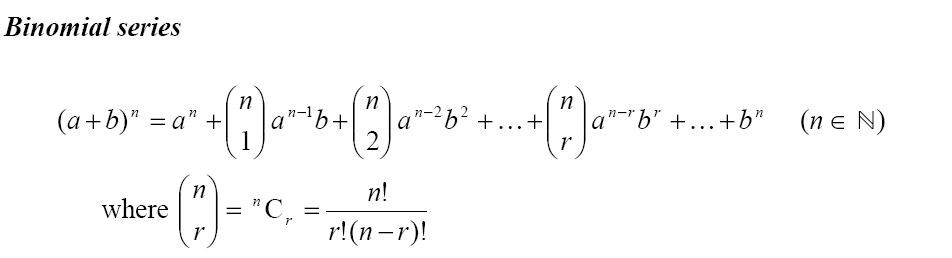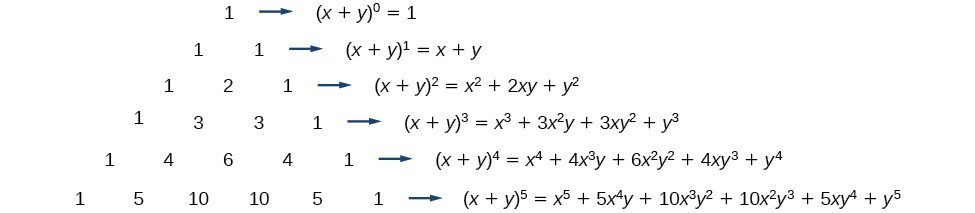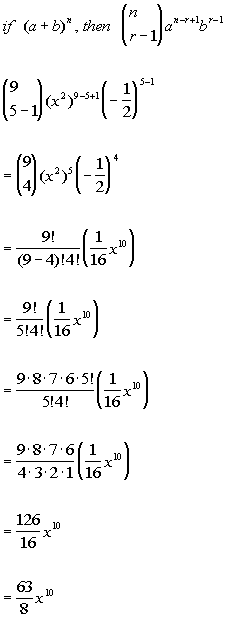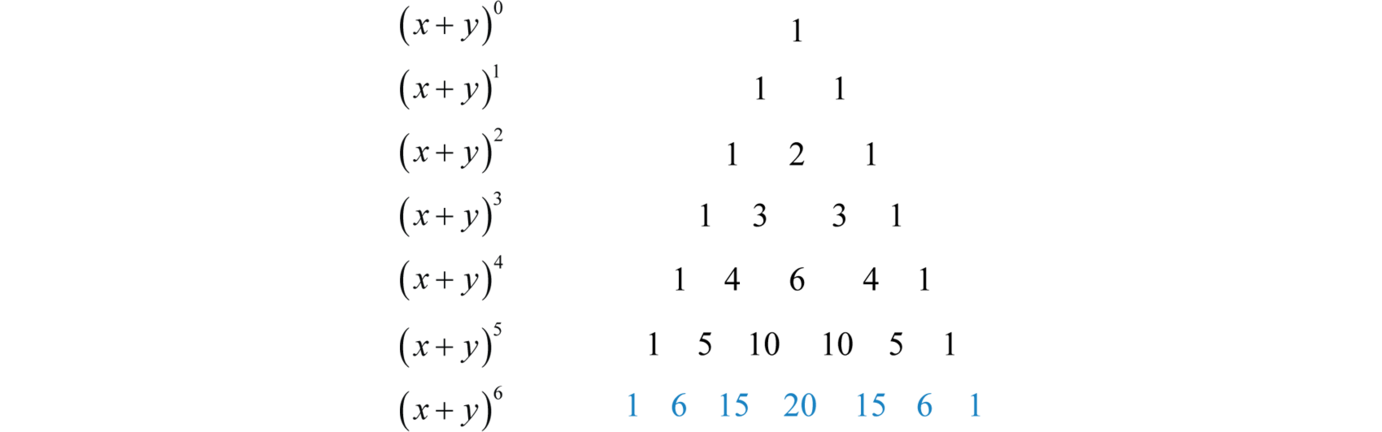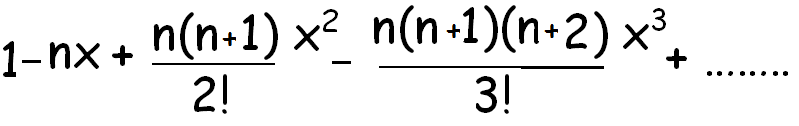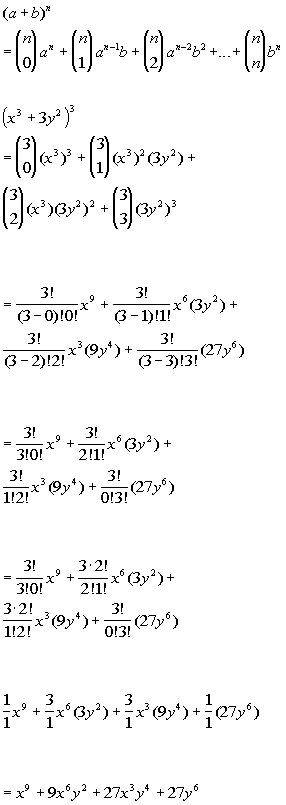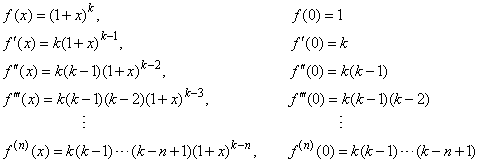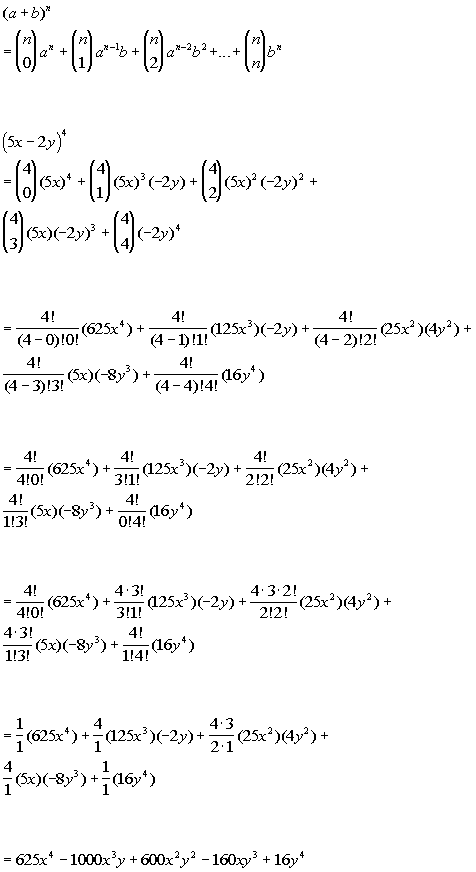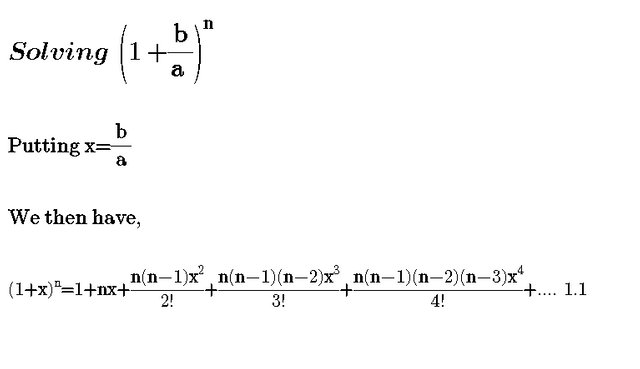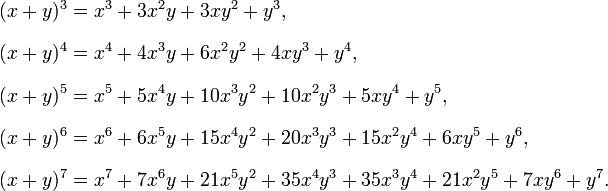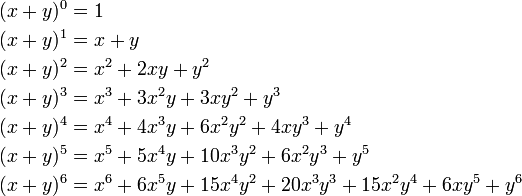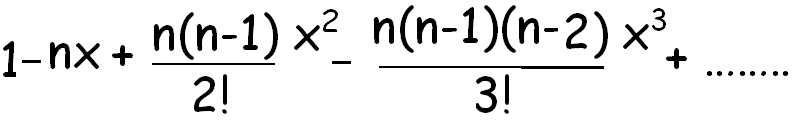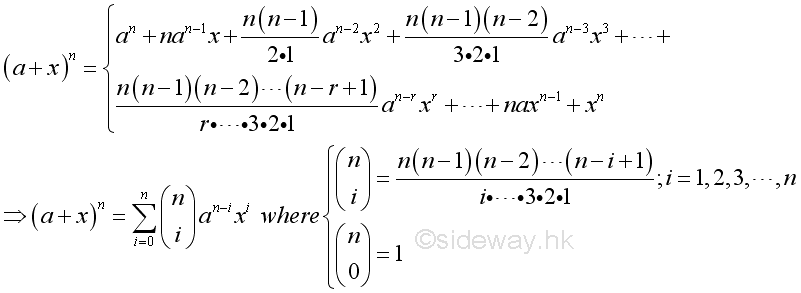Binomial Expansion Formula 1xn

The variables m and n do not have numerical coefficients. The power of the binomial is 9. Binomial theorem as the power increases the expansion becomes lengthy and tedious to calculate.
binomial expansion formula (1+x)^n

1 1 2 1 3 1 2 3 2 12 1 32 1 2 3 2 5 2 123 1 33.

Binomial expansion formula 1xn. Here we are going to see the formula for the b inomial expansion formula for 1 plus x whole power n. The binomial expansion of 1xn 1 x n is. The binomial has two properties that can help us to determine the coefficients of the remaining terms. Expand 4 2x 6 in ascending powers of x up to the term in x 3.

Binomial expansion formula for 1 plus x whole power n. Determine the values of x x and n n. Here it represents the product of all the whole numbers between 1 and n. Learn about all the details about binomial theorem like its definition properties applications etc.

Xy1 xy xy2 x2 2xy y2 xy3 x3 3x2y 3xy2 y3 properties of the binomial expansion x y n. This means use the binomial theorem to expand the terms in the brackets but only go as high as x 3. A b n a n n c 1a n 1 b n c 2a n 2 b 2 n c n 1ab n 1 b n. We can write down the binomial expansion of 1xn 1 x n as.

Binomial expansion formula for 1 plus x whole power n. So the given numbers are the outcome of calculating the coefficient formula for each term. Xynsumk0n n choose k xn k yk also recall that the factorial notation n. 2 x 4 2 4 1 x2 4 can be expanded by binomial theorem since.

The expression of the binomial theorem formula is given as follows. The binomial theorem states that where n is a positive integer. Some expansions are as follows. 1 1 2 1 3 1 2 3 2 1 2 1 3 2 1 2 3 2 5 2 1 2 3 1 3 3.

In elementary algebra the binomial theorem or binomial expansion describes the algebraic expansion of powers of a binomialaccording to the theorem it is possible to expand the polynomial x y n into a sum involving terms of the form ax b y c where the exponents b and c are nonnegative integers with b c n and the coefficient a of each term is a specific positive integer depending. A binomial expression that has been raised to a very large power can be easily calculated with the help of binomial theorem. Therefore the number of terms is 9 1 10. And download binomial theorem pdf lesson from below.