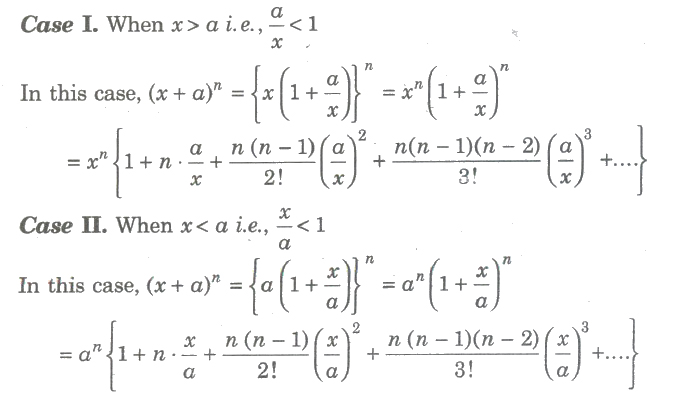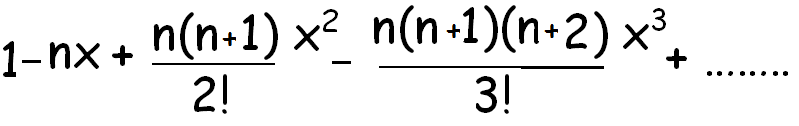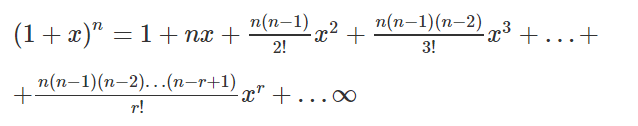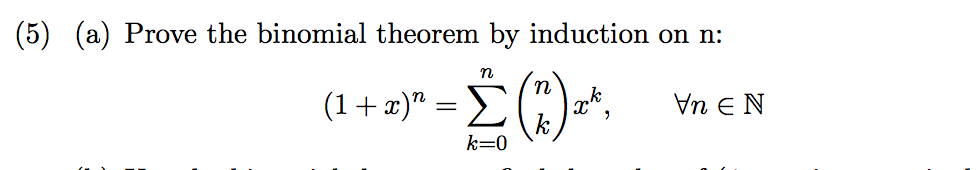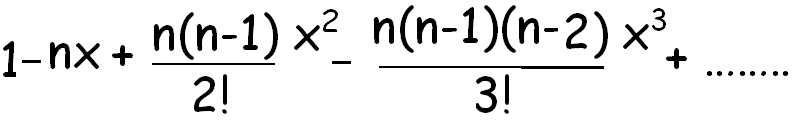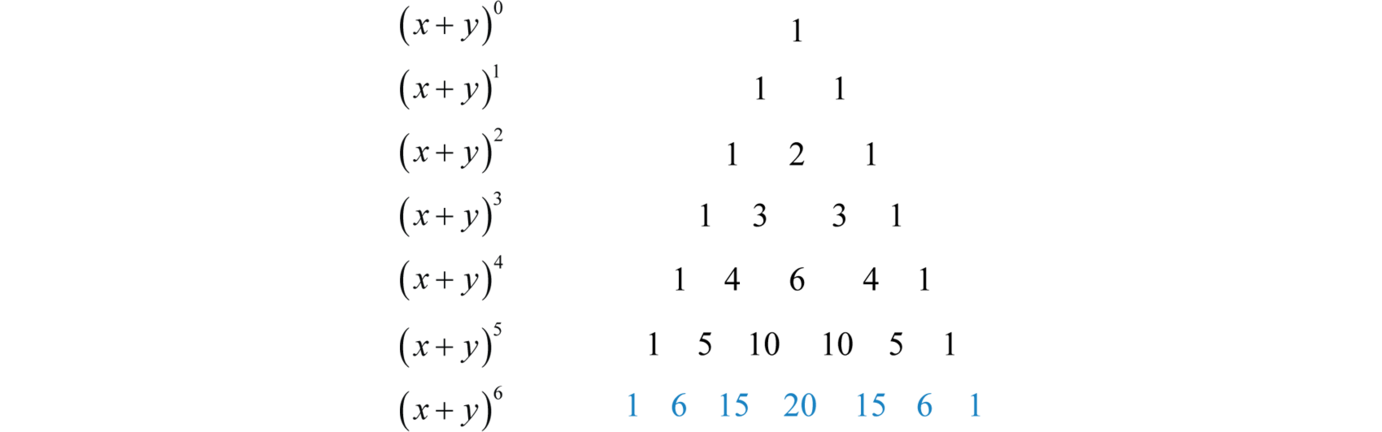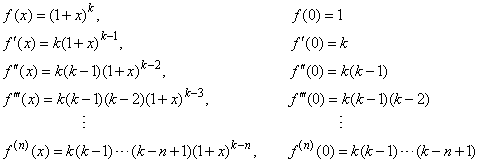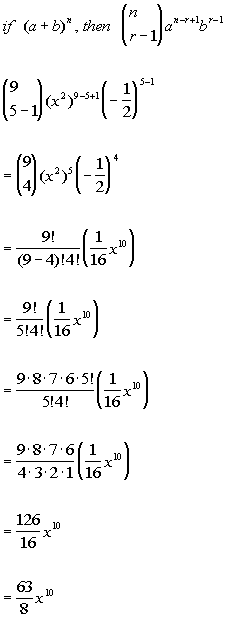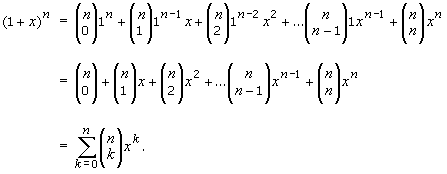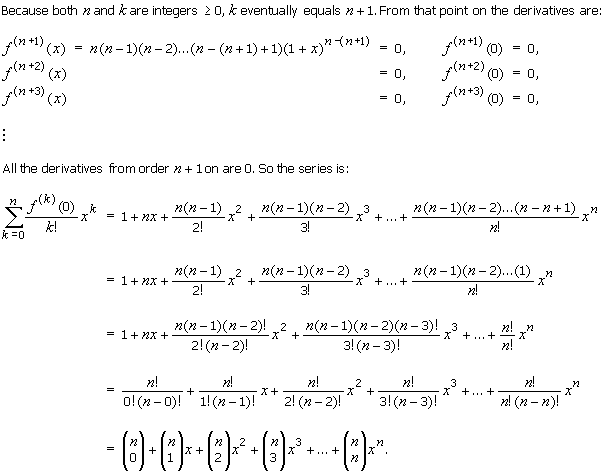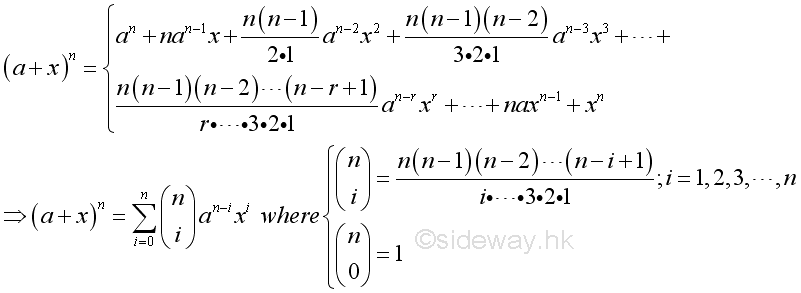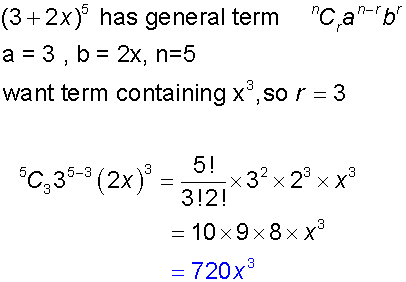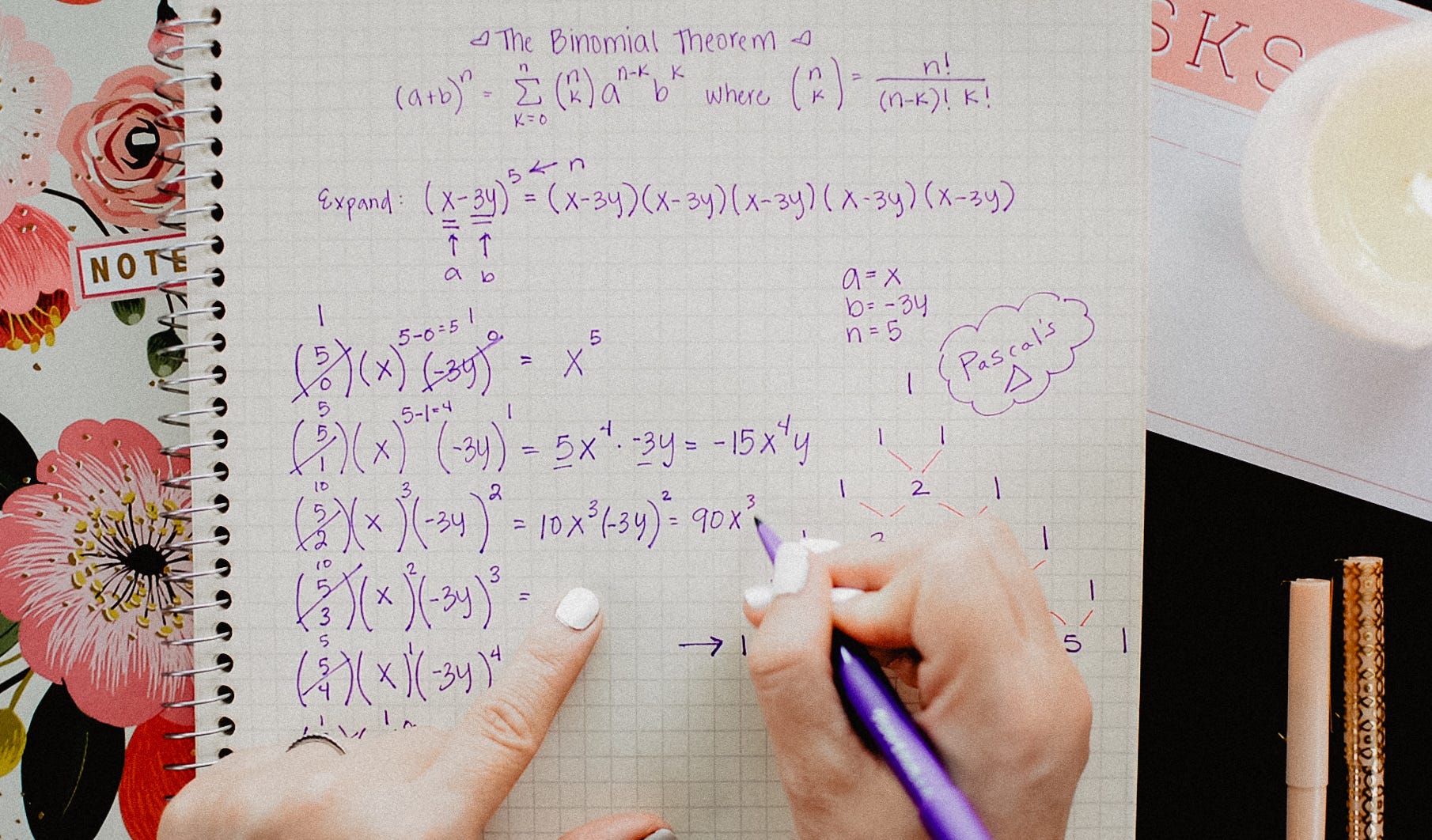Binomial Theorem Formula 1xn

Binomial theorem statement that for any positive integer n the n th power of the sum of two numbers a and b may be expressed as the sum of n 1 terms of the form. Here we are going to see the formula for the b inomial expansion formula for 1 plus x whole power n. First we can drop 1 n k as it is always equal to 1.
binomial theorem formula (1+x)^n

A binomial is an algebraic expression containing 2 terms.

Binomial theorem formula 1xn. In the sequence of terms the index r takes on the successive values 0 1 2 n. 1 1n n it gets more accurate the higher the value of n that formula is a binomial right. And quite magically most of what is left goes to 1 as n goes to infinity. A b n a n n c 1a n 1 b n c 2a n 2 b 2 n c n 1ab n 1 b n.

When we have negative signs for either power or in the middle we have negative signs for alternative terms. So lets use the binomial theorem. We sometimes need to expand binomials as follows. The binomial theorem states that where n is a positive integer.

A b 0 1a b 1 a ba b 2 a 2 2ab b 2a b 3 a 3 3a 2 b 3ab 2 b 3a b 4 a 4 4a 3 b 6a 2 b 2 4ab 3 b 4a b 5 a 5 5a 4 b 10a 3 b 2 10a 2 b 3 5ab 4 b 5clearly doing this by. 4 can be expanded by binomial theorem since x 2. Expand 4 2x 6 in ascending powers of x up to the term in x 3. With just those first few terms we get e 27083.

1 x n 1 x n 1 x n 1 x n. In elementary algebra the binomial theorem or binomial expansion describes the algebraic expansion of powers of a binomialaccording to the theorem it is possible to expand the polynomial x y n into a sum involving terms of the form ax b y c where the exponents b and c are nonnegative integers with b c n and the coefficient a of each term is a specific positive integer depending. For example x y is a binomial. This means use the binomial theorem to expand the terms in the brackets but only go as high as x 3.

The coefficients called the binomial coefficients are defined by the formula.