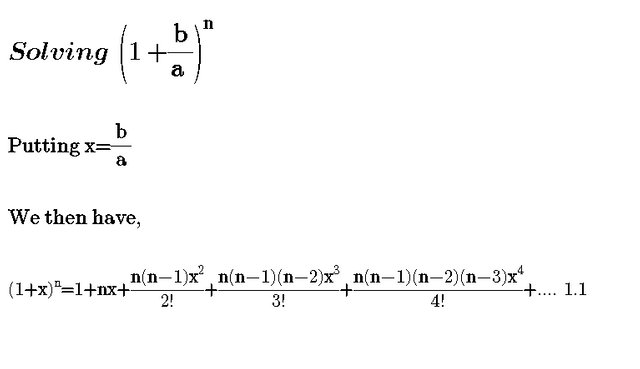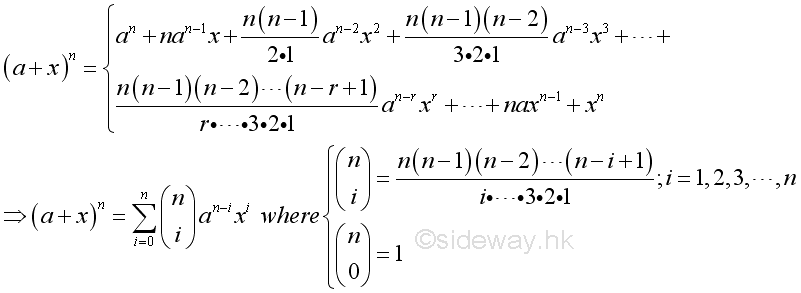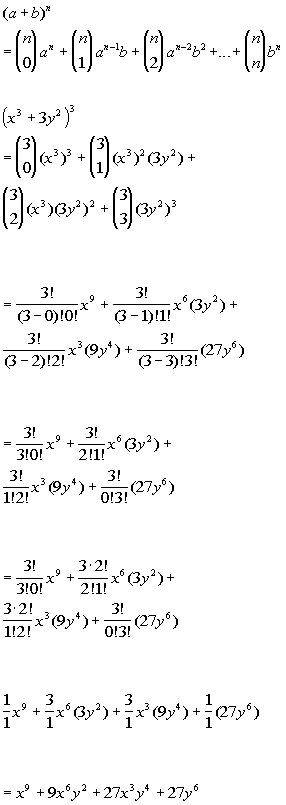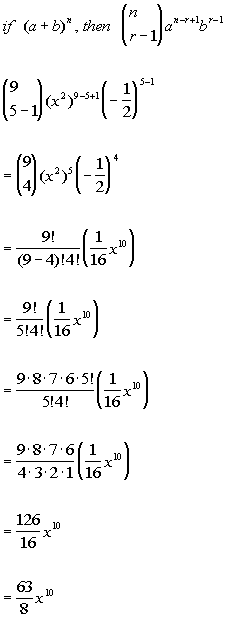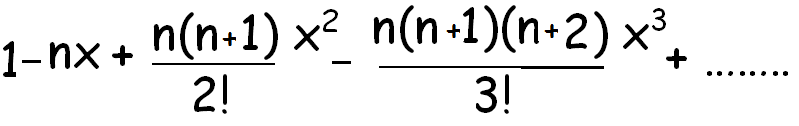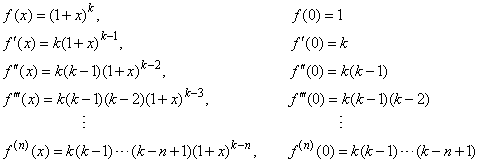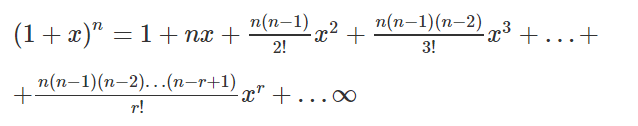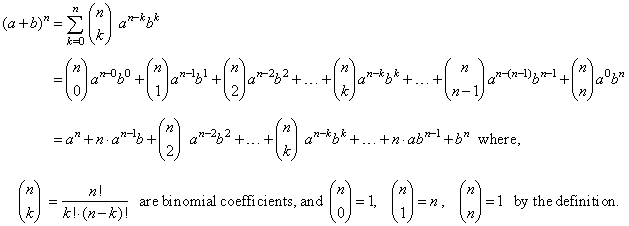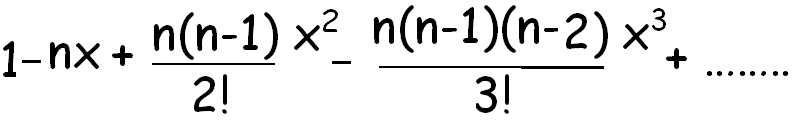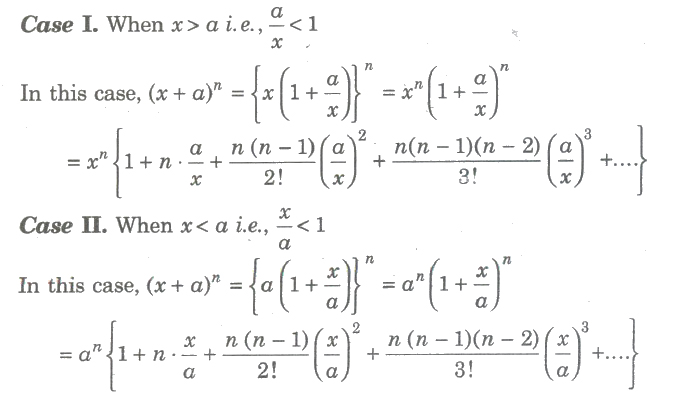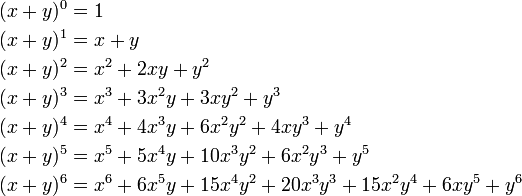Binomial Formula 1xn

1 n 1.

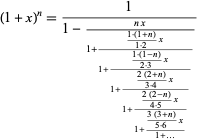
Binomial formula 1xn. It is the coefficient of the x k term in the polynomial expansion of the binomial power 1 x n and it is given by the formula for example the fourth power of 1 x is. X 2 n n 1 n 2 3. In the binomial expansion formula for 1 xn 1 nx nn 1 2. The coefficients called the binomial coefficients are defined by the formula.

In elementary algebra the binomial theorem or binomial expansion describes the algebraic expansion of powers of a binomialaccording to the theorem it is possible to expand the polynomial x y n into a sum involving terms of the form ax b y c where the exponents b and c are nonnegative integers with b c n and the coefficient a of each term is a specific positive integer depending. Binomial theorem statement that for any positive integer n the nth power of the sum of two numbers a and b may be expressed as the sum of n 1 terms of the form. This means use the binomial theorem to expand the terms in the brackets but only go as high as x 3. Expand 4 2x 6 in ascending powers of x up to the term in x 3.

The result would be. Simplify the exponents for each term of the expansion. Expand using the binomial theorem 1 x3. The binomial theorem states.

X2 nn1n2 3. Substitute x for x and 1 2 for n. A b n a n n c 1a n 1 b n c 2a n 2 b 2 n c n 1ab n 1 b n. We can write down the binomial expansion of 1xn 1 x n as 1 n 1x nn1 2.

Use the binomial expansion theorem to find each term. This is true for all real values of n n although there are conditions on x x. X n n 1 2. In mathematics the binomial coefficients are the positive integers that occur as coefficients in the binomial theoremcommonly a binomial coefficient is indexed by a pair of integers n k 0 and is written.

In the sequence of terms the index r takes on the successive values 0 1 2 n.